New Blogger Initiative: Integer Context Cards

For Week 2 of the “New Math Blogger Initiative” (or is it an “initiation?” hmmmmm) I decided to learn how to embed a document using Scribd and show something that I am proud to share!

If you read my Made4Math post from last week (Math Cards) you know I like “multi-purpose” tools. I haven’t been teaching Middle School too long, in the grand scheme of things, and when I first had the opportunity to introduce Integers to a class of very low sixth graders (all Level 1 on the state test) I knew that putting them into context would make all the difference. So. . . what are some contexts for integers? Well, there’s temperature, and altitude, and money. . .? I brainstormed long and hard and came up with quite a list.

Without further ado, my very first Scribd document!

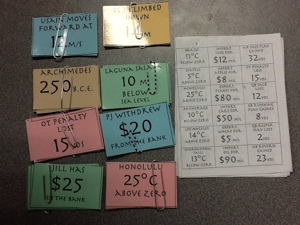
Integer Context Cards

View this document on Scribd

(Hmmmm. Rats! The font changed when I uploaded the document. The original was in Herculanum, a very cool looking ALL CAPS font, so now it appears that I don’t know my capitalization rules – oh well.)

There are a total of eighteen different contexts with six cards for each one. Some are “stretching it” a bit, but still reasonable. Note: for altitude, one of the cards is for Arlington, Washington where my school is located, so you might want to “personalize” that one. 🙂

I made one copy of each page on a different color of copy paper to make them easier to sort and then had them laminated, cut, and paperclipped in sets of six. (I only made one set for the entire class, but you can certainly create duplicates, especially if you have a very large class.)

Order, Order, Order

Phase 1: After a brief exposure to a few of the cards, we started our first activity with the cards. My students were already assigned to groups of six. We actually went out into a space in the hall for this.) Each group received a different set of cards, passed them out amongst the group members, and silently “raced” to put themselves in order from least to greatest. Once a group was done, they ALL had to raise their hands. After I checked for accuracy, they turned in their set and grabbed a new one. (The first year I did this I checked the groups off on a master sheet, but the following years I just trusted their memory – “We already did that set.”) The goal was to accurately get through as many sets as they could in the time allotted. Often enough, groups were in too much of a hurry to read carefully enough to identify the “key words” that signified whether their value was positive or negative. Getting a “no” when their hands were raised definitely encouraged them to take their time a bit more.

Phase 2: The next activity took it just a bit further. Groups (of three this time) had a sheet of number lines. Each time they received a new set of cards they had to “fairly accurately” plot and label all six values (along with zero if it wasn’t in the set) on a number line. Choosing a scale was challenging for some of the sets (especially with the first group of students.)

(See the cool font? Oh, well.)

Integer Operations in Context

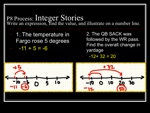
A few weeks later in the year, my seventh grade class was working on operations with integers. I printed the Integer Card sheets four to a page and created little packets for students to share. (See the image above.) Using a “Think Pair Share” type of model, I posed questions using the people, places, or things on the cards and students had to write a math sentence, model the problem on a number line, and find the value (first on their own paper, then with a partner on a mini-whiteboard.) A big key was writing the math sentence as opposed to just finding the value. I wanted them to make the connection so that when they saw a “naked numbers” problem they could try to connect it to the contexts we worked with in class.

We initially focused on addition and subtraction situations:
(**The white text is shown first. After the Think-Pair-Share on whiteboards I reveal the number sentence and diagram and move onto the next problem.**)

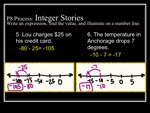
Next we moved onto subtraction in “finding differences” contexts, as well as multiplication and division. I dropped the “number line” requirement, although we did end up sharing it on some of the more challenging multiplication/division situations. (Again, the white text for each problem is given first, TPS, then the yellow answer is revealed, discussed, and we move on to the next problem.)

In subsequent years I used the Integer Operation activities with my sixth grade classes as we introduced this seventh grade concept in the Spring after the state test. During “Review Activities” time in class I had small groups create original “stories” along with their associated number sentences, from the cards, but I think I would like to make that a more integral part of the initial learning as well.

Ahhhhh, context! Even if it is really “pseudo context,” in this situation students have something to grab onto that helps them make sense of the integer operations as opposed to a mercurial “set of rules to follow.” On the other hand, it is THROUGH these experiences that students begin to create their OWN rules about the patterns involved in integer operations, but only when the concepts “make sense” to THEM! I think we are finding a bit of EMU right there. 🙂

Note: There are multiple slides for each operation, and if I got my act together I might copy and paste them all into one slide show and try to attach them, but that would take a higher level of understanding on Scribd than I currently possess, as the slides are all now on my iPad, and I am just sharing screenshots.

Flashback Friday: “Sharing” in Sums

When my own kids were VERY young, we used to play “finger math.” Hold up some fingers on each hand and ask “How much is 2 and 3?” Of course, in time it changed, bit by bit so that “2 and 3” became “2 + 3,” holding up the fingers became their job, and then there were no fingers at all. The specific memory involves asking my daughter “How much is 3 and 5?” Right away she said “Eight!” Since we had been playing for a little while, I teased her, saying “No, it can’t be eight. You told me 4 and 4 was eight!” She replies with “Look, Mama, you give one from the five over to the three and then it’s four and four!”

Why don’t students automatically think that way more often?

I know, some do, but it seems that addition is so often accomplished one of three ways:
-It is a “known fact” they are able to recall immediately.
-They “stack the numbers” (either on paper or mentally) and add using the algorithm.
-Ummm, I’m too lazy so I’ll use a calculator.

Now, occasionally students will use alternative mental strategies, but often only IF the numbers are “compatible” to begin with, such as 25 + 75. Why don’t we encourage them to MAKE the numbers “more compatible,” if they can? Who wouldn’t rather add 40 + 63 than 39 + 64? What about 50 + 75 instead of 48 + 77? How can we improve our students’ “computational FLEXibility” instead of just focusing on their “computational ABility?”

Enduring Mathematical Understanding doesn’t come from knowing how to apply an algorithm, it comes from looking for alternatives, strategies, and shortcuts that arise from a deeper sense of number!

Flashback Friday: Half and Double

When my son was about six years old we would “play math” when we were in the car, or getting dinner ready, or just “playing.” I remember asking him what 7 x 8 was, and hearing a reply that went something like this: “Well, 7 x 8 is the same as 14 x 4, and 14 x 4 is the same as 28 x 2, so. . . 56!” It was not quite what I expected, but then I recalled a brief conversation we had had some time earlier involving the number 12.

(Paraphrased)
Son: “3 x 4 is 12, and so is 6 x 2.”
Me: “Yes. . .?”
Son: “Does that always work?”
Me: “What?”
Son: “That if you double 3 you get 6, and half of 4 is 2.”
Me: “Well, what do you think?”

I could see the gears turning as he thought about it in his mind – picturing the four groups of three changing into the two groups of six. I don’t recall the resolution of the discussion, but apparently it was enough to satisfy him so that it became a strategy that he began to use on a regular basis. I am certain that I did not encourage it as a “method,” just an interesting occurrence.

A few weeks after the “7 x 8” question, I asked it again, expecting that he might remember “56” from his previous “derivation.” Here’s what I got: “Well, 7 x 8 is the same as 14 x 4, and 14 x 4 is the same as 28 x 2, so. . . 56!” He showed exactly the same enthusiasm for “solving the puzzle” that he had a few weeks earlier, not recollecting that he had, in fact, solved it before.

Contrast that with the child who has memorized 7 x 8 = 56, and would be able to repeat it back in the blink of an eye. Who has more Enduring Mathematical Understanding?